Compartments and TADs detection¶
Here, we present the analysis to detect the compartments in Mouse B and iPS cells. In this example, we will use the GC-content (guanine-cytosine content) to identify which bins belong to the A or B compartments. The percentage of bases that are either guanine or cytosine on a DNA strand correlates directly with gene density and is a good measure to identify open and close chromatine.
Note: Compartments are detected on the full genome matrix.
from pytadbit.parsers.hic_parser import load_hic_data_from_bam
from pytadbit.parsers.genome_parser import get_gc_content, parse_fasta
from pickle import load
reso = 200000
base_path = 'results/fragment/{0}_both/03_filtering/valid_reads12_{0}.bam'
bias_path = 'results/fragment/{0}_both/04_normalizing/biases_{0}_both_{1}kb.biases'
rich_in_A = get_gc_content(parse_fasta('genome/Mus_musculus-GRCm38.p6/Mus_musculus-GRCm38.p6.fa'),
by_chrom=True ,resolution=reso, n_cpus=8)
Loading cached genome
Compartments¶
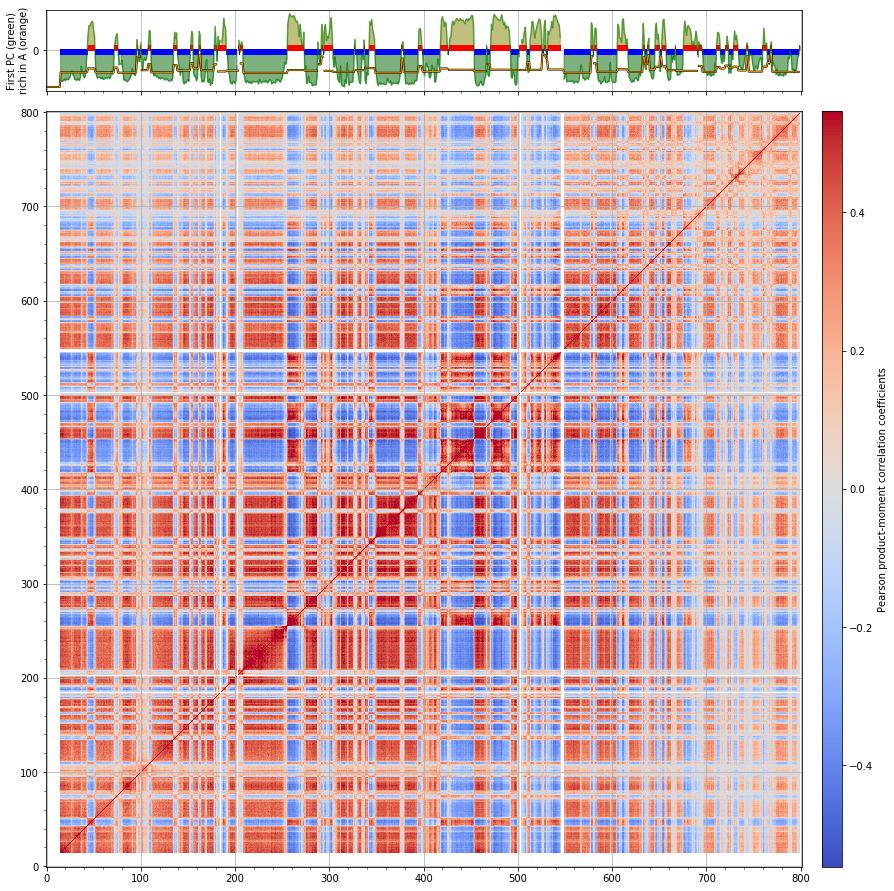
Mouse B cells¶
cell = 'mouse_B'
hic_data = load_hic_data_from_bam(base_path.format(cell),
resolution=reso,
biases=bias_path.format(cell, reso // 1000),
ncpus=8)
(Matrix size 13641x13641) [2020-02-06 12:04:07] - Parsing BAM (122 chunks) [2020-02-06 12:04:08] .......... .......... .......... .......... .......... 50/122 .......... .......... .......... .......... .......... 100/122 .......... .......... .. 122/122 - Getting matrices [2020-02-06 12:06:28] .......... .......... .......... .......... .......... 50/122 .......... .......... .......... .......... .......... 100/122 .......... .......... .. 122/122
! mkdir -p results/fragment/$cell\_both/05_segmenting
chrname = 'chr3'
corr = hic_data.find_compartments(show_compartment_labels=True,
show=True, crms=[chrname], vmin='auto', vmax='auto', rich_in_A=rich_in_A,
savedata='results/fragment/{0}_both/05_segmenting/compartments_{1}_{2}.tsv'.format(cell, chrname, reso),
savedir='results/fragment/{0}_both/05_segmenting/eigenvectors_{1}_{2}'.format(cell, chrname, reso))
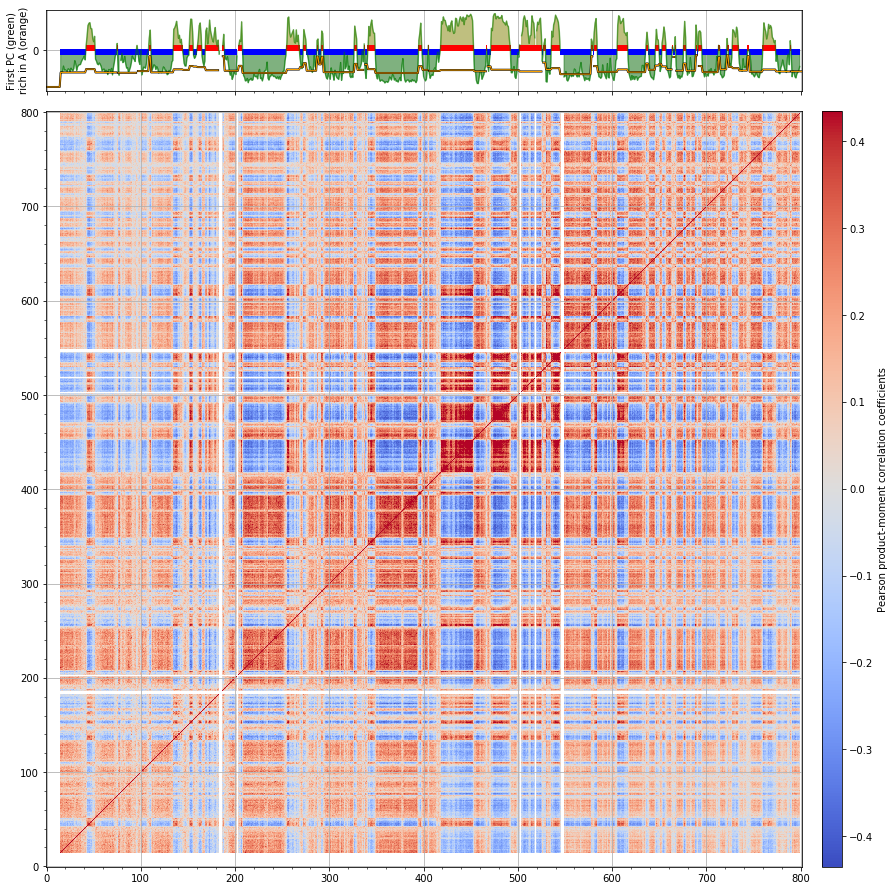
Mouse iPS cells¶
cell = 'mouse_PSC'
hic_data = load_hic_data_from_bam(base_path.format(cell),
resolution=reso,
biases=bias_path.format(cell, reso // 1000),
ncpus=8)
(Matrix size 13641x13641) [2020-02-06 12:20:31] - Parsing BAM (122 chunks) [2020-02-06 12:20:32] .......... .......... .......... .......... .......... 50/122 .......... .......... .......... .......... .......... 100/122 .......... .......... .. 122/122 - Getting matrices [2020-02-06 12:22:08] .......... .......... .......... .......... .......... 50/122 .......... .......... .......... .......... .......... 100/122 .......... .......... .. 122/122
! mkdir -p results/fragment/$cell\_both/05_segmenting
chrname = 'chr3'
corr = hic_data.find_compartments(show_compartment_labels=True,
show=True, crms=[chrname], vmin='auto', vmax='auto', rich_in_A=rich_in_A,
savedata='results/fragment/{0}_both/05_segmenting/compartments_{1}_{2}.tsv'.format(cell, chrname, reso),
savedir='results/fragment/{0}_both/05_segmenting/eigenvectors_{1}_{2}'.format(cell, chrname, reso))
Compare¶
The assignments of the compartments for the two cell types are stored in two different files:
! head -n 20 results/fragment/mouse_B_both/05_segmenting/compartments_chr3_200000.tsv
## CHR chr3 Eigenvector: 1 # start end rich in A type chr3 16 44 0.40 B chr3 45 52 0.50 A chr3 53 72 0.40 B chr3 73 76 0.53 A chr3 77 96 0.39 B chr3 97 98 0.82 A chr3 99 100 0.82 B chr3 101 101 nan A chr3 102 108 0.46 B chr3 109 111 0.62 A chr3 112 135 0.40 B chr3 136 139 0.59 A chr3 140 153 0.44 B chr3 154 156 0.64 A chr3 157 162 0.51 B chr3 163 164 0.87 A chr3 165 178 0.46 B chr3 179 181 0.61 A
! head -n 20 results/fragment/mouse_PSC_both/05_segmenting/compartments_chr3_200000.tsv
## CHR chr3 Eigenvector: 1 # start end rich in A type chr3 16 42 0.40 B chr3 43 52 0.49 A chr3 53 75 0.40 B chr3 76 76 nan A chr3 77 96 0.39 B chr3 97 97 nan A chr3 98 109 0.43 B chr3 110 111 0.84 A chr3 112 135 0.40 B chr3 136 145 0.48 A chr3 146 152 0.47 B chr3 153 156 0.57 A chr3 157 160 0.56 B chr3 161 165 0.54 A chr3 166 169 0.54 B chr3 170 183 0.46 A chr3 184 184 nan B chr3 188 189 0.84 A
In another folder, we also saved the coordinates of each computed eigenvector:
! ls -lh results/fragment/mouse_B_both/05_segmenting/eigenvectors_chr3_200000
total 52K -rw-r--r-- 1 dcastillo dcastillo 49K Feb 6 12:08 chr3_EigVect1.tsv
Note: In this file the first line shows the eigenvector index with it’s corresponding eigenvalue (the first column should always be the one you selected, even if it is not the first eigenvector).
Then there are the coordinates of the eigenvectors. In the first column, the coordinates correspond to the assignment of the A and B compartments, positive values for A compartments and negative values for B compartments.
! head -n 20 results/fragment/mouse_B_both/05_segmenting/eigenvectors_chr3_200000/chr3_EigVect1.tsv
# EV_1 (199.3674) EV_2 (38.9365) EV_3 (22.7067) nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan -0.04705877433867864 0.0008416946845418325 -0.0418514300736033 -0.04570124930041132 0.004910131406689665 -0.03832275686221951 -0.04591426453743422 0.002039448345766754 -0.035967872719506695 -0.044857688854588844 0.003962351416820969 -0.04230275892744377
Load eigenvectors coordinates from files:
from builtins import next
fh = open('results/fragment/mouse_B_both/05_segmenting/eigenvectors_chr3_200000/chr3_EigVect1.tsv')
header = next(fh)
ev1_B = []
for line in fh:
evc1, evc2, evc3 = line.split()
ev1_B.append(float(evc1))
fh = open('results/fragment/mouse_PSC_both/05_segmenting/eigenvectors_chr3_200000/chr3_EigVect1.tsv')
header = next(fh)
ev1_PSC = []
for line in fh:
evc1, evc2, evc3 = line.split()
ev1_PSC.append(float(evc1))
diff = []
for i in range(len(ev1_B)):
diff.append(ev1_B[i] - ev1_PSC[i])
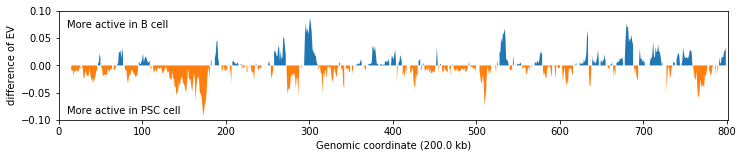
Spot changes in activity¶
Plot the difference between each eigenvector along chromosome
from matplotlib import pyplot as plt
plt.figure(figsize=(12, 2))
plt.text(10, 0.07, 'More active in B cell')
plt.fill_between(range(len(diff)), diff, 0, where=[i>0 for i in diff])
plt.text(10, -0.09, 'More active in PSC cell')
plt.fill_between(range(len(diff)), diff, 0, where=[i<0 for i in diff])
plt.xlim(0, len(diff))
plt.ylim(-0.1, 0.1)
plt.ylabel('difference of EV')
_ = plt.xlabel('Genomic coordinate (%s kb)' % (reso / 1000))
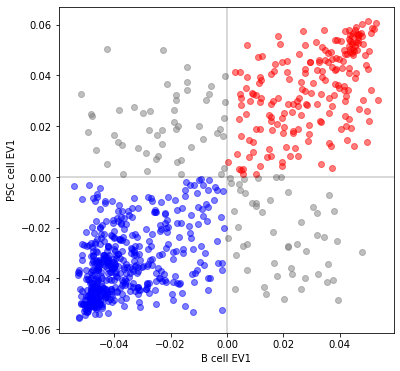
Correlate eigenvectors¶
plt.figure(figsize=(6, 6))
for i in range(len(ev1_B)):
if ev1_B[i] > 0 and ev1_PSC[i] > 0:
plt.plot(ev1_B[i], ev1_PSC[i], 'ro', alpha=0.5)
elif ev1_B[i] < 0 and ev1_PSC[i] < 0:
plt.plot(ev1_B[i], ev1_PSC[i], 'bo', alpha=0.5)
else:
plt.plot(ev1_B[i], ev1_PSC[i], 'o', color='grey', alpha=0.5)
plt.axhline(0, color='k', alpha=0.2)
plt.axvline(0, color='k', alpha=0.2)
plt.xlabel('B cell EV1')
_ = plt.ylabel('PSC cell EV1')
TADs¶
Now, we move to the TADs detection. In this notebook we will detect TAD borders at 100kbp resolution.
from pytadbit import Chromosome
from pytadbit.parsers.hic_parser import load_hic_data_from_bam
base_path = 'results/fragment/{0}_both/03_filtering/valid_reads12_{0}.bam'
bias_path = 'results/fragment/{0}_both/04_normalizing/biases_{0}_both_{1}kb.biases'
reso = 100000
cel1 = 'mouse_B'
cel2 = 'mouse_PSC'
hic_data1 = load_hic_data_from_bam(base_path.format(cel1),
resolution=reso,
region='chr3',
biases=bias_path.format(cel1, reso // 1000),
ncpus=8)
hic_data2 = load_hic_data_from_bam(base_path.format(cel2),
resolution=reso,
region='chr3',
biases=bias_path.format(cel2, reso // 1000),
ncpus=8)
(Matrix size 1601x1601) [2020-02-06 12:36:22] - Parsing BAM (101 chunks) [2020-02-06 12:36:24] .......... .......... .......... .......... .......... 50/101 .......... .......... .......... .......... .......... 100/101 . 101/101 - Getting matrices [2020-02-06 12:36:28] .......... .......... .......... .......... .......... 50/101 .......... .......... .......... .......... .......... 100/101 . 101/101 (Matrix size 1601x1601) [2020-02-06 12:36:54] - Parsing BAM (101 chunks) [2020-02-06 12:36:55] .......... .......... .......... .......... .......... 50/101 .......... .......... .......... .......... .......... 100/101 . 101/101 - Getting matrices [2020-02-06 12:36:59] .......... .......... .......... .......... .......... 50/101 .......... .......... .......... .......... .......... 100/101 . 101/101
chrname = 'chr3'
crm = Chromosome(chrname)
crm.add_experiment('mouse_B',
hic_data=[hic_data1.get_matrix(focus='chr3')],
norm_data=[hic_data1.get_matrix(focus='chr3',normalized=True)],
resolution=reso)
crm.add_experiment('mouse_PSC',
hic_data=[hic_data2.get_matrix(focus='chr3')],
norm_data=[hic_data2.get_matrix(focus='chr3',normalized=True)],
resolution=reso)
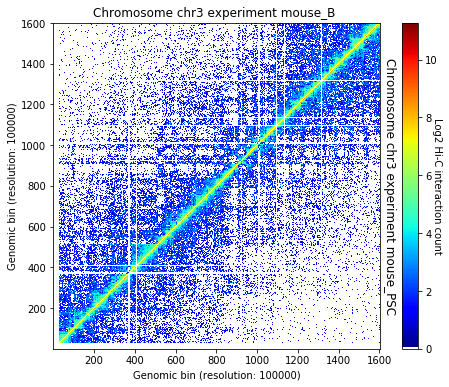
crm.visualize([('mouse_B', 'mouse_PSC')])
TAD caller algorithms¶
TADbit¶
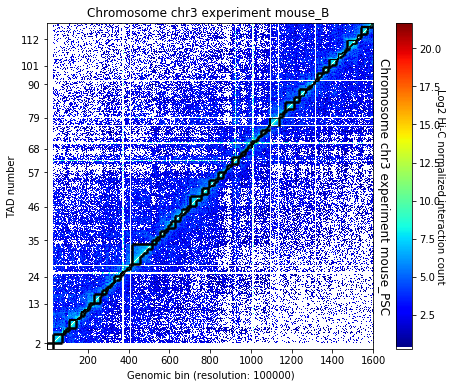
TADbit is the original TAD caller algorithm TADbit is a breakpoint detection algorithm that returns the optimal segmentation of the chromosome under BIC-penalized likelihood. The model assumes that counts have a Poisson distribution and that the expected value of the counts decreases like a power-law with the linear distance on the chromosome.
crm.find_tad(['mouse_B', 'mouse_PSC'], n_cpus=8)
crm.visualize([('mouse_B', 'mouse_PSC')], normalized=True, paint_tads=True)
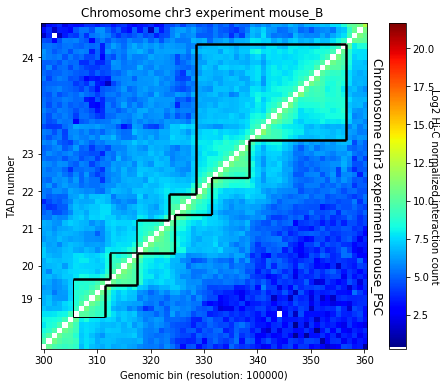
crm.visualize([('mouse_B', 'mouse_PSC')], normalized=True, paint_tads=True, focus=(300, 360))
B = crm.experiments['mouse_B']
PSC = crm.experiments['mouse_PSC']
crm.experiments
[Experiment mouse_B (resolution: 100 kb, TADs: 96, Hi-C rows: 1601, normalized: visibility), Experiment mouse_PSC (resolution: 100 kb, TADs: 118, Hi-C rows: 1601, normalized: visibility)]
TopDom¶
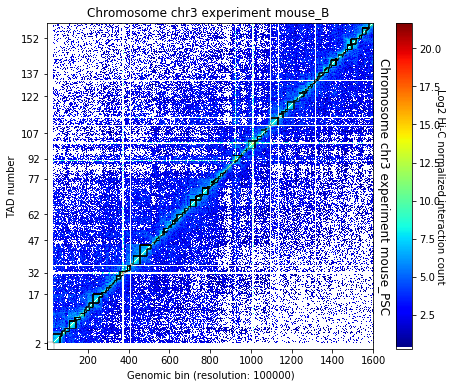
TopDom identifies TAD borders based on the assumption that contact frequencies between regions upstream and downstream of a border are lower than those between two regions within a TAD. The algorithm only depends on a single parameter corresponding to the window size. The algorithm provides a measure (from 0 to 10) of confidence on the accuracy of the border detection (https://www.ncbi.nlm.nih.gov/pubmed/26704975).
crm.find_tad(['mouse_B', 'mouse_PSC'], n_cpus=8, use_topdom=True)
crm.visualize([('mouse_B', 'mouse_PSC')], normalized=True, paint_tads=True)
crm.visualize([('mouse_B', 'mouse_PSC')], normalized=True, paint_tads=True, focus=(300, 360))
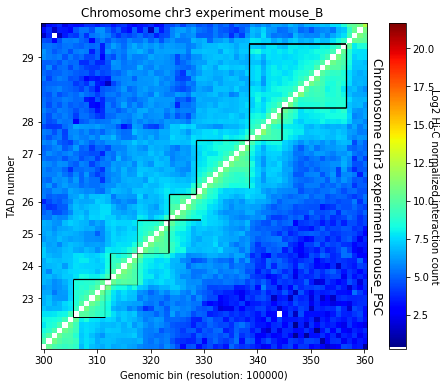
Insulation score¶
Insulation score (Crane et al. 2015 https://doi.org/10.1038/nature14450) can be used to build an insulation profile of the genome and, with a simple transformation, to identify TAD borders.
from pytadbit.tadbit import insulation_score, insulation_to_borders
First we need to normalize the matrices by visibility and by decay:
hic_data1.normalize_hic()
hic_data1.normalize_expected()
hic_data2.normalize_hic()
hic_data2.normalize_expected()
iterative correction
- copying matrix
- computing biases
rescaling to factor 1
- getting the sum of the matrix
=> 1553.816
- rescaling biases
iterative correction
- copying matrix
- computing biases
rescaling to factor 1
- getting the sum of the matrix
=> 1570.990
- rescaling biases
The two important parameter to define are the window size, the distance from the diagonal and the delta. - the square size should be 500 kb as close as possible from the diagonal - the delta is to look for increases in insulation around a given bin. Should be around 100 kb (in out case we define it as 200 kb as we are working at 100 kb resolution, and working with only one bin is a bit to little)
wsize = (1, 4)
insc1, delta1 = insulation_score(hic_data1, [wsize], resolution=100000, normalize=True, delta=2)
insc2, delta2 = insulation_score(hic_data2, [wsize], resolution=100000, normalize=True, delta=2)
- computing insulation in band 1-4 - computing insulation in band 1-4
/home/dcastillo/miniconda2/envs/py3_tadbit/lib/python3.7/site-packages/numpy/core/fromnumeric.py:3335: RuntimeWarning: Mean of empty slice. out=out, **kwargs)
Once defined the insulation score and the values of delta can be used to search for borders.
borders1 = insulation_to_borders(insc1[wsize], delta1[wsize], min_strength=0.1)
borders2 = insulation_to_borders(insc2[wsize], delta2[wsize], min_strength=0.1)
Currently the representation is not available in TADbit as for the other methods, but we can easily plot it:
plt.figure(figsize=(10, 4))
plt.subplot(2, 1, 1)
plt.title('B cell')
l1 = plt.plot([insc1[(wsize)].get(i, float('nan')) for i in range(max(insc1[(wsize)]))], label='Insulation score')
l2 = plt.plot([delta1[(wsize)].get(i, float('nan')) for i in range(max(insc1[(wsize)]))],
alpha=0.3, label='Delta value')
for b, c in borders1:
l3 = plt.plot([b] * 2, [-2, -2.3], color='darkgreen', alpha=c, lw=4, label='Border strength')
plt.grid()
plt.axhline(0, color='k')
plt.ylim(-2.5, 2)
plt.xlim(300, 360)
plt.legend(l1 + l2 + l3, [l.get_label() for l in l1 + l2 + l3], frameon=False, bbox_to_anchor=(1.3, 0.6))
plt.subplot(2, 1, 2)
plt.title('PSC')
plt.plot([insc2[(wsize)].get(i, float('nan')) for i in range(max(insc2[(wsize)]))])
plt.plot([delta2[(wsize)].get(i, float('nan')) for i in range(max(insc2[(wsize)]))], alpha=0.3)
for b, c in borders2:
plt.plot([b] * 2, [-2, -2.3], color='darkgreen', alpha=c, lw=4)
plt.grid()
plt.axhline(0, color='k')
plt.ylim(-2.5, 2)
_ = plt.xlim(300, 360)
plt.tight_layout()
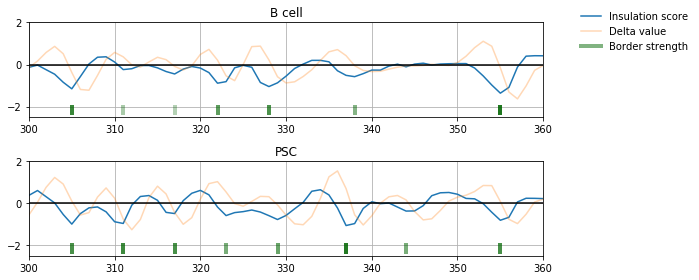
Comparison of TAD borders¶
The TAD borders can be aligned, using a simple reciprocal best hit strategy:
ali = crm.align_experiments(['mouse_B', 'mouse_PSC'], max_dist=reso)
In the plots below, each arc represents a TAD. Between two consecutive arcs the triangle mark the border. This triangle is colored depending on the confidence of the TAD border call.
ali.draw(ymax=3)

ali.draw(focus=(1, 350), ymax=3)
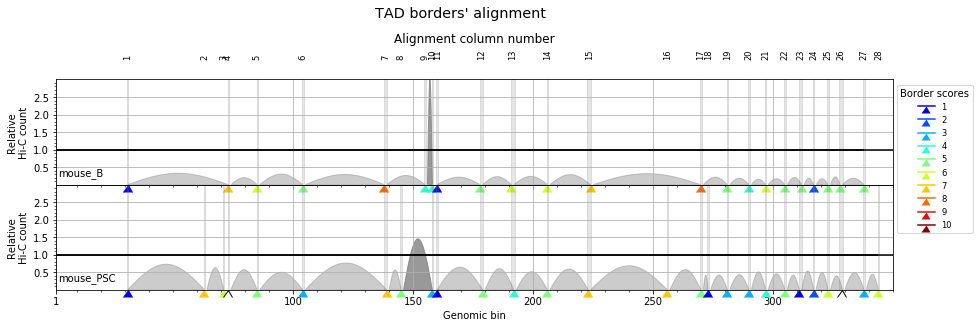
Statistical significance of the TAD borders alignments¶
In order to asses how well two experiments align, or how conserved are the TAD borders between two experiments, we can compare the overlap between our experiments with the overlap of simulated random distributions of TAD borders.
ali, stats = crm.align_experiments(['mouse_B', 'mouse_PSC'], randomize=True)
print(ali)
Alignment shown in 100 Kb (2 experiments) (scores: 0 1 2 3 4 5 6 7 8 9 10) mouse_B:| 31| ---- | ---- | 73| 85| 104| 138| ---- | 155| 158| 160| 178| 191| 206| 224| ---- | 270| ---- | 281| 290| 297| 305| 312| 317| 323| 328| 338| ---- | 356| ---- | ---- | ---- | 382| 389| ---- | 407| 410| 419| 454| ---- | 508| 510| 512| ---- | 522| 530| 535| 543| ---- | 552| 561| ---- | 574| ---- | 591| 600| 608| 612| 625| 635| ---- | ---- | ---- | 660| ---- | 673| ---- | ---- | ---- | 692| 700| 731| 751| 761| 789| 798| 801| ---- | 819| 830| 837| 849| ---- | 861| ---- | 870| 877| 880| 883| 889| ---- | 895| 900| ---- | 908| ---- | ---- | ---- | ---- | ---- | 949| 959| 963| ---- | 967| 976| ---- | 986| ---- | 1020| 1027| ---- | 1047| 1051| ---- | ---- | ---- | 1075| ---- | 1084| 1093| 1097| ---- | 1134| 1136| 1154| ---- | ---- | 1169| 1175| ---- | 1211| ---- | 1221| 1228| 1235| ---- | 1257| 1264| 1270| 1275| 1280| 1291| 1298| 1301| 1307| 1314| 1316| ---- | 1326| 1333| ---- | ---- | 1352| 1359| 1369| 1378| 1384| 1393| 1418| ---- | 1428| ---- | 1444| 1448| 1452| 1459| ---- | 1470| 1490| ---- | ---- | 1521| 1528| 1540| 1546| ---- | 1575| 1581| ---- | 1602 mouse_PSC:| 31| 63| 71| 73| 85| 104| 139| 145| ---- | 158| 160| 179| 192| 206| 223| 256| 270| 273| 281| 290| 297| 305| 311| 317| 323| 329| 338| 344| 356| 362| 370| 376| 382| 389| 405| 407| 410| 418| 454| 489| 508| 510| 512| 514| 522| 530| 535| ---- | 547| 552| 560| 572| ---- | 585| 591| ---- | 607| 612| 625| 635| 640| 648| 653| 660| 663| 674| 681| 687| 690| ---- | 700| 731| 752| 760| 789| 799| 801| 808| 820| 831| 838| 849| 856| 862| 868| 870| ---- | 880| 883| 888| 891| ---- | ---- | 905| 907| 914| 921| 931| 936| 943| 949| 959| 962| 965| 967| 976| 979| ---- | 988| 1019| ---- | 1030| 1047| 1051| 1057| 1060| 1069| 1076| 1082| ---- | 1093| ---- | 1099| 1134| 1136| ---- | 1156| 1163| 1169| ---- | 1177| 1211| 1218| ---- | ---- | 1235| 1243| 1258| ---- | 1271| ---- | 1280| 1292| 1298| 1301| 1307| 1314| 1316| 1319| 1327| 1333| 1339| 1346| 1352| 1358| ---- | 1377| 1385| 1392| 1418| 1425| ---- | 1430| 1444| ---- | 1453| ---- | 1462| 1470| ---- | 1496| 1516| 1521| 1528| 1539| 1546| 1566| 1575| ---- | 1583| 1602
This analysis returns an alignment score between 0 and 1 (0: no match, 1: all borders aligned), a p-value (usually equal zero), the proportion of borders conserved in the second experiment, and the proportion of borders conserved in the first experiment:
stats
The history saving thread hit an unexpected error (OperationalError('database is locked')).History will not be written to the database.
(0.4696132596685082, 0.0, 0.872, 0.8980891719745223)
print('Alignment score: %.3f, p-value: %.4f\n proportion of borders of T0 found in T60: %.3f, of T60 in T0 %.3f' % stats)
Alignment score: 0.470, p-value: 0.0000 proportion of borders of T0 found in T60: 0.872, of T60 in T0 0.898
Save Chromosome object (with TAD definition)¶
crm.save_chromosome('results/fragment/chr3.tdb')
Extra: choosing the best resolution to call TAD borders¶
TopDom and the methodology based on insulation score are relatively fast computationally and allow to call TAD borders at very high resolution. However being able to call TAD borders at high resolution does not mean that we should do it. As the resolution increases, so does the noise.
In order to assess which is the best resolution in order to call TAD borders, a good strategy is to test the consistency of several resolutions.
In the example below, we use the methodology based on the insulation score as it is the fastest (tadbit strategy is almost not usable bellow 20 kb). We compare the number of TAD borders that are shared (plus-minus one bin) between the two replicates (iPS and B cells).
from pytadbit.parsers.hic_parser import load_hic_data_from_bam
from pytadbit.tadbit import insulation_score, insulation_to_borders
base_path = 'results/fragment/{0}_both/03_filtering/valid_reads12_{0}.bam'
cel1 = 'mouse_B'
cel2 = 'mouse_PSC'
borders = {}
resos = [5000, 10000, 20000, 30000, 40000, 50000, 60000, 80000, 100000, 150000, 200000]
for c in ['chr%d' % cs for cs in range(1, 20)] + ['chrX']:
borders[c] = {}
for reso in resos:
hic_data1 = load_hic_data_from_bam(base_path.format(cel1),
resolution=reso,
region=c,
ncpus=8, verbose=False)
hic_data2 = load_hic_data_from_bam(base_path.format(cel2),
resolution=reso,
region=c,
ncpus=8, verbose=False)
hic_data1.normalize_hic(silent=True)
hic_data1.normalize_expected()
hic_data2.normalize_hic(silent=True)
hic_data2.normalize_expected()
wsize = (1, max(2, 500000 // reso))
delta = max(1, 100000 // reso)
insc1, delta1 = insulation_score(hic_data1, [wsize], resolution=100000, normalize=True, delta=delta)
insc2, delta2 = insulation_score(hic_data2, [wsize], resolution=100000, normalize=True, delta=delta)
borders1 = insulation_to_borders(insc1[wsize], delta1[wsize], min_strength=0.1)
borders2 = insulation_to_borders(insc2[wsize], delta2[wsize], min_strength=0.1)
borders[c][reso] = borders1, borders2
- computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2 - computing insulation in band 1-100 - computing insulation in band 1-100 - computing insulation in band 1-50 - computing insulation in band 1-50 - computing insulation in band 1-25 - computing insulation in band 1-25 - computing insulation in band 1-16 - computing insulation in band 1-16 - computing insulation in band 1-12 - computing insulation in band 1-12 - computing insulation in band 1-10 - computing insulation in band 1-10 - computing insulation in band 1-8 - computing insulation in band 1-8 - computing insulation in band 1-6 - computing insulation in band 1-6 - computing insulation in band 1-5 - computing insulation in band 1-5 - computing insulation in band 1-3 - computing insulation in band 1-3 - computing insulation in band 1-2 - computing insulation in band 1-2
We align TAD borders and keep the proportion of borders aligned between cell types
from pytadbit.alignment import align
scores = {}
props1 = {}
props2 = {}
for c in borders:
scores[c] = []
props1[c] = []
props2[c] = []
for reso in resos:
ali = align([[t[0] for t in b] for b in borders[c][reso]], max_dist=1)
props1[c].append(ali[0][2])
props2[c].append(ali[0][3])
scores[c].append(ali[0][1])
We plot the results, as boxplots to group the values of each chromosomes:
from functools import reduce
plt.figure(figsize=(12, 5))
bp = plt.boxplot([reduce(lambda x, y: x+ y,
[(props1[c][i], props2[c][i]) for c in props1])
for i in range(len(resos))], positions=resos, widths=2000)
plt.plot([sum(m.get_xdata()) / 2 for m in bp['medians']],
[0m.get_ydata()[0] for m in bp['medians']], color='grey', alpha=0.5)
plt.xlim(0, 205000)
plt.xticks(resos, [str(reso / 1000) + 'kb' for reso in resos], rotation=90)
plt.ylabel('Proportion of aligned borders\nPSC vs B cell (all chromosomes)')
plt.xlabel('Resolution at which TAD borders are called')
plt.grid()
plt.tight_layout()
plt.show()
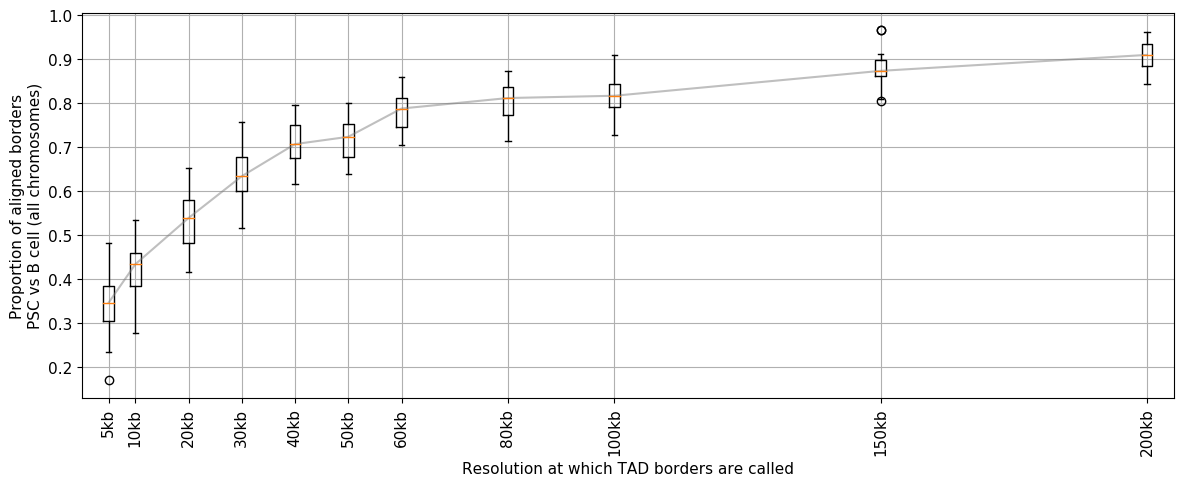
In the case of these experiments it seems that looking for TAD borders bellow 50 kb is dangerous, as very few are reproducible. Calling TAD borders at 100 kb resolution might be here a good idea.

